最近听到的一个最简单的解释,这个其实算是入门之入门,但是由于这个入门把很多人难住了,我自己也是花了很长时间才理解的,不过今天听到的这个方法,明显简单太多了.给觉得难以入门的人说一下.
不讲高深的数学概念,不写复杂的数学公式,如何解释清楚这个问题.但是,数学是避不开的,但是会简单很多很多,请相信我.
比如先有一个图和一个点,这个点X=-6.84,Y=46.84,我们知道X^2的导数2X,这个没问题吧,所以当前点导数是-13.68,如果我们X移动-13.68,那么Y会怎样,越来越大,所以导数总是指向数值增大的方向的,记住这一点.
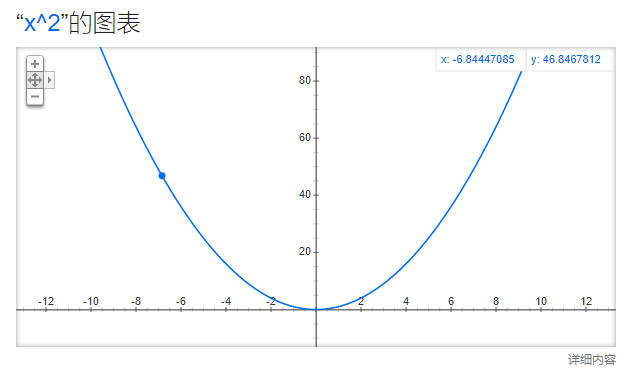
OK,那么我们目标是找减少的方向,因为就反着移动呗,但是-6.84 - (-13.68) = 6.84,那么,Y没任何变化,步子迈的太大,直接越过了.
但是我们现在不知道步子加多少可以到达Y最低(当然,你现在要装作不知道.),然后开始计算了,为了不引入超级复杂的东西,所以先以最简单的方法来解决.
# 先假设x是-10.24
x = -10.24
# 原函数公式
# f(x) = x ** 2
# 导数公式
# f(x)' = 2 * x
# 每次步子大小
lr = 0.01
# 进行走10步
for i in range(10):
# 往更靠小点的位置靠近.
x = x - (lr * (2 * x))
# 输出新的X,以及新的Y.
print(x,x ** 2)上面的代码,每次往导数的反方向,即数据减少的方向迈进0.01步,执行看看.
-10.0352 100.70523904
-9.834496 96.717311574016
-9.637806079999999 92.88730603568494
-9.445049958399999 89.20896871667182
-9.256148959231998 85.67629355549161
-9.071025980047358 82.28351233069412
-8.889605460446411 79.02508524239865
-8.711813351237483 75.89569186679967
-8.537577084212733 72.8902224688744
-8.36682554252848 70.00376965910698
找到了一个比原来好很多的x,如果迭代100次,结果可能又好很多,没错,着就是梯度下降法.
-1.5330314756872818 2.350185505447925
-1.5023708461735361 2.2571181594321867
-1.4723234292500653 2.167736280318672
-1.442876960665064 2.0818939236180527
-1.4140194214517627 1.9994509242427778
-1.3857390330227275 1.920272667642764
-1.358024252362273 1.8442298700041104但是,这还不够用,我们现在知道,0是我们理想数值,但是不代表最低就是0,甚至可能不是为了找最低,而是找和原函数损失最小.
我们先生成一堆伪数据,使用如下公式.
y = ax+b+c,其中a,b都是固定的,c是随机的,一定范围的.
import random
dataset = []
a = 12
b = 0.5
for x in range(100):
y = (a * x) + b + random.uniform(0.1, 20)
dataset.append(([x, y]))
print(dataset)但是我们要假设其实是不知道a,b的,我们要求他出来,就假设我们求得是a,b,假设我们预测出的a和b分别是w,c,也就是如果有一条公式,满足wx+c ≈ f(x),那么我们就胜利了,怎么猜,随机肯定不行,所以要梯度下降法.
原则围绕导数的反方向前进,即损失最小,这里损失怎么计算,就是wx + c - f(x),那么我们预测出来的就越靠谱,那么总误差怎么计算呢,把所有误差加起来不就行了,不过注意正负,所以我们把他平方起来,即(wx + c - f(x)) ^ 2,OK,程序写一下LOSS函数.
w = 0 # 预测的a
c = 0 # 预测的b
loss = 0
for x in range(100):
loss += ((w * x) + c - dataset[x][1]) ** 2
print(loss)我得到的大概5000万左右的loss,这个数字太大了,不容易量化,不如除以个总个数.
print(loss / 100)这样大概50万左右.
为了梯度下降,必须求导数,其中 (wx + c - f(x)) ^ 2 的导数是2(wx + c - f(x)),对w的导数即c,f(x)是常数,导数结果为0,wx导数结果x,那么就是 2(wx + c - f(x))*x,对c的导数,注意c也有前面的系数,即1*c,所以结果是2(wx + c - f(x))*1,他们导数也出来了.
OK,概念有了,先进行一步预测.
w = 0 # 预测的a
c = 0 # 预测的b
loss = 0
for x in range(100):
# 求损失
loss += ((w * x) + c - dataset[x][1]) ** 2
loss = loss / 100
# 求导数
w_gradient = (2 * ((w * x) + c - dataset[x][1])) * x
c_gradient = (2 * ((w * x) + c - dataset[x][1])) * 1
w_gradient = w_gradient / 100
c_gradient = c_gradient / 100
# 往合适的方向移动,步子大小lr = 0.001
lr = 0.001
w = w - lr * w_gradient
c = c - lr * c_gradient
print([loss / 100, w, c])然后尝试逼近更多次数,比如100次,完整程序和结果如下,结果很相近.
import random
dataset = []
a = 12
b = 0.5
for x in range(100):
y = (a * x) + b + random.uniform(0.1, 20)
dataset.append(([x, y]))
w = 0 # 预测的a
c = 0 # 预测的b
for step in range(100):
loss = 0
for x in range(100):
# 求损失
loss += ((w * x) + c - dataset[x][1]) ** 2
loss = loss / 100
# 求导数
w_gradient = (2 * ((w * x) + c - dataset[x][1])) * x
c_gradient = (2 * ((w * x) + c - dataset[x][1])) * 1
w_gradient = w_gradient / 100
c_gradient = c_gradient / 100
# 往合适的方向移动,步子大小lr = 0.001
lr = 0.001
w = w - lr * w_gradient
c = c - lr * c_gradient
print([loss / 100, w, c])
结果:
...
[7.908794887083978e-06, 12.013155768965193, 0.1213450077673252]
[7.908793844868221e-06, 12.013155770477857, 0.12134500778260464]
[7.908793006974678e-06, 12.01315577169398, 0.1213450077948887]
[7.90879233334438e-06, 12.013155772671693, 0.12134500780476459]